4-1. If \(n\) is a positive integer, then \(n!\) is the product of the first \(n\) positive integers. What is the only integer \(n > 0\) satisfying \(n! + n! = (2n)!\)?
4-2. If the roots of \(ax^2 + bx - 2025 = 0\) are reciprocals, what is the value of \(a\)?
Let's just set \(c=–2025\) and use the quadratic formula to solve for \(x_1\) and \(x_2\), then since \(x_1=\frac{1}{x_2}\), we can solve the ensuing equation for \(a\). Here's the procedure:
\[ax^2+bx+c=0\]
\[x_1 = \frac{–b+\sqrt{b^2-4ac}}{2a}\]
\[x_2 = \frac{–b-\sqrt{b^2-4ac}}{2a}\]
\[x=\frac{1}{x_2}\]
\[\frac{–b+\sqrt{b^2-4ac}}{2a}=\frac{2a}{–b-\sqrt{b^2-4ac}}\]
\[(2a)(2a)=(–b+\sqrt{b^2-4ac})(–b-\sqrt{b^2-4ac})\]
\[4a^2=b^2-(b^2-4ac)\]
\[4a^2=b^2-b^2+4ac\]
\[4a^2=4ac\]
\[\frac{4a^2}{4a}=c\]
\[a=c\]
Since \(c=–2025\), \(\boxed{a=–2025}\).
4-3. Circle O has a radius of length \(4\). Points A and B are chosen on the circle so that \(\measuredangle AOB = 30°\). What is the area of the region inside the circle that's formed by all points that are closer to A than to B?
4-4. Numbers like \(123\) and \(321\) are called reversals if we can get one from the other by reversing the order of the digits. What is the larger of two positive reversals whose product is \(71685\)?
You can solve this via trial and error, and I did that and arrived at the solution pretty quickly, but here I'll use algebra. We can represent any \(3\)-digit number algebraically as \(100a+10b+c\) and its reversal as \(100c+10b+a\). To solve for \(a\), \(b\) and \(c\), we just multiply these two \(3\)-digit numbers algebraically and set the answer to \(71,685\). I used the Perplexity AI bot to write a Javascript function to find \(a\), \(b\) and \(c\) by performing a brute-force search for solutions to the equation if \(a\), \(b\) and \(c\) could only be integers between \(1\) and \(9\), and used the OneCompiler website to run the script. Here's the equation, and under it the Javascript and the result of running the script:
\[(100a+10b+c)(100c+10b+a) = 71685\]
function solveEquation() {
for (let a = 1; a <= 9; a++) {
for (let b = 1; b <= 9; b++) {
for (let c = 1; c <= 9; c++) {
let leftSide = 10001 * a * c + 100 * (a**2 + b**2 + c**2) + 1010 * (a*b + b*c);
if (leftSide === 71685) {
console.log(`a = ${a}, b = ${b}, c = ${c}`);
}
}
}
}
}
solveEquation();
a = 1, b = 3, c = 5
a = 5, b = 3, c = 1
Given that the question asked for the larger of the two reversals, the solution is \(\boxed{531}\).
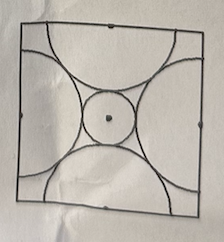4-5. Four congruent semicircles inscribed in a square have their centers at the midpoints of the sides of the square. A small circle that has its center at the center of the square is also tangent to each of the semicircles, as shown. If the radius of the small circle is \(1\), what is the area of the square?
4-6. For what integer \(k\) does \((\sqrt{2}-1)^n = -239 + k\sqrt{2}\) for some positive integer \(n\)?